A1 AlphaQCM

《AlphaQCM: Alpha Discovery in Finance with Distributional Reinforcement Learning》
https://icml.cc/virtual/2025/poster/46517

通讯作者

朱柯-香港大学-**Welcome to My Homgpage

问题

搜索Alpha因子，MDP的非平稳性与奖励稀疏性

方法

从可能带有偏差的分位数中计算出**无偏的方差估计
融合用于分位数学习的IQN主干网络与用于Q值近似的DQN算法
Pasted image 20251201194115.png

实验

基线方法比较、消融实验

数据集：三个不同的股票池：(1) 最大的 300 只股票（沪深 300），(2) 最大的 500 只股票（中证 500），以及 (3) 在上海和深圳证券交易所上市的所有股票（全市场）

基线方法：Alpha101（人工设计的公式化阿尔法）、MLP, XGBoost, LightGBM（基于机器学习的非公式化阿尔法）、 GP w/o filter, GP w/ filter（基于遗传编程的公式化阿尔法）、 PPO w/ filter, AlphaGen（基于强化学习的公式化阿尔法）

评估指标：IC等

评分维度	核心指标 / 规则	目的
核心性能	测试集 IC 均值（越高越好）	衡量阿尔法的预测能力
结果可靠性	IC 标准差（越小越好）	衡量方法的稳定性
泛化能力	跨股票池 IC 一致性（越稳定越好）	衡量方法在复杂市场中的适应性
实用价值	可解释性（公式化 > 非公式化）	确保方法能应用于实际金融场景
对比公平性	验证集统一调优超参数	保证不同方法的对比公平

价值

解决序列决策问题中的非平稳性和奖励稀疏性

补充

“阿尔法”这个词源于资产定价模型中的一个关键概念：

贝塔： 衡量投资组合相对于整个市场波动性的指标，代表的是系统性风险带来的收益。这是一种被动的、跟随市场的收益。
阿尔法： 衡量投资组合超越市场基准（经贝塔调整后）的超额收益。它代表了通过主动管理和技能所带来的附加价值。

因此，一个成功的“阿尔法因子”的目标，就是帮助投资者发现并捕获这种“阿尔法”收益，即跑赢市场的部分。

1. 公式化阿尔法因子

定义： 由一个简单、明确、可解释的数学公式表达的因子。
示例：
- 动量因子： （当前价格 - N天前的价格）/ N天前的价格。该值高表明股票处于上升趋势，可能继续上涨。
- 反转因子： 与动量相反，认为过去跌幅过大的股票可能会反弹。
- 价值因子： 如市净率（P/B Ratio），认为低市净率的股票被低估。
优点：
- 可解释性强： 逻辑清晰，易于理解。
- 泛化能力强： 不易过拟合，在不同的市场和时期可能都有效。
- 信任度高： 在金融机构中广泛接受和使用。

2. 非公式化阿尔法因子

定义： 通常由复杂的机器学习模型（如深度学习神经网络） 以“端到端”的方式生成。模型本身就是一个阿尔法因子。
工作原理： 输入历史数据，模型直接输出预测信号。这个信号背后的逻辑可能非常复杂且不透明。
优点： 可能发现人脑难以察觉的复杂、非线性模式。
缺点：
- 黑箱问题： 难以理解其决策依据，导致信任度低。
- 过拟合风险高： 模型可能只是记住了数据中的噪声，而非真实规律。
- 泛化能力差： 在市场环境变化时可能突然失效。

特性	阿尔法因子
本质	预测未来资产价格走势的信号或指标。
目标	获取超越市场基准的超额收益。
输入	历史市场数据（价格、成交量、财务报表数据等）。
输出	一个代表未来看涨或看跌预期的数值信号。
理想形态	协同的公式化阿尔法因子——即一组可解释、能相互增强的简单数学规则。

概念	气象预报比喻	数学定义与关系
Q函数	平均温度。它是所有可能温度的一个加权平均。`Q(s,a) = 平均温度`	期望累积回报。`Q(s,a) = 𝔼[Z(s,a)]`。它是回报分布Z的数学期望（平均值）。
分位数	温度分布的临界点。例如： - τ=0.1分位数（22°C）：有10%的几率温度低于22°C。 - τ=0.5分位数（25°C）：有50%的几率温度低于25°C，这就是中位数。 - τ=0.9分位数（28°C）：有90%的几率温度低于28°C。	回报分布的τ分位数。对于随机变量Z(s,a)，其τ分位数 `θ_τ` 满足：`P(Z(s,a) <= θ_τ) = τ`。它描述了回报分布的形状和范围。

背景

发现具有协同效应的公式化阿尔法因子

将整体阿尔法发现机制概念化为一个非平稳、奖励稀疏的马尔可夫决策过程

应对非平稳性与奖励稀疏性

非公式化阿尔法因子->协同的公式化阿尔法因子

公式化：它们可以用简单的公式表达，这通常使其紧凑、可解释且可泛化

协同：允许通过某些可解释的模型（例如线性模型）将它们组合成一个元阿尔法因子

找公式化阿尔法因子方法

遗传编程方法GP，

问题：GP方法的搜索空间巨大，其规模随输入特征和运算符的数量呈指数级增长。

RL方法

AlphaGen方法：将阿尔法发现问题重新定义为为一个特定的马尔可夫决策过程MDP寻找最优策略的任务，强化学习

问题：非平稳性问题，奖励稀疏性（大多数被发现的阿尔法因子都很弱，导致奖励为零）忽略分布信息


1. 奖励稀疏性	难以高效地探索搜索空间。
2. 非平稳性问题	样本效率和收敛性能
3. 忽略分布信息	完全忽略了已观察到的表达式以及后续阿尔法构建过程中蕴含的复杂分布信息，导致阿尔法发现过程效率低下且不稳定。

方法

将寻找协同公式化Alpha因子的过程，重新构建为一个序列决策问题

AlphaQCM方法——一种专为高效搜索协同公式化阿尔法而设计的分布式强化学习新框架

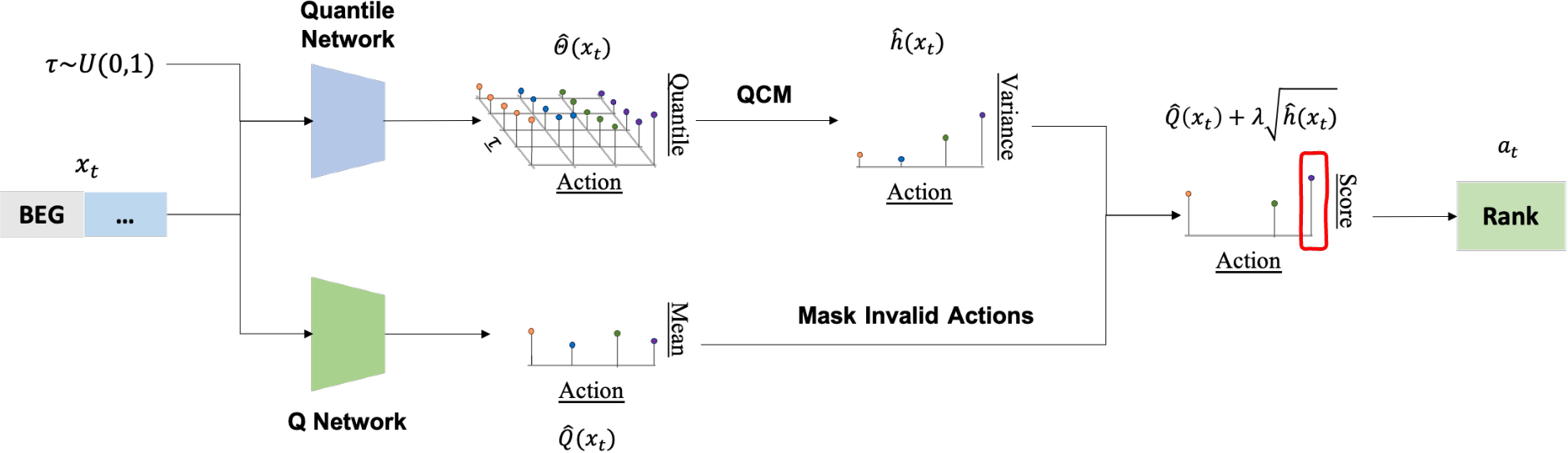
首先通过Q网络与分位数网络分别学习Q函数与分位数；

继而运用分位数条件矩估计法从可能存在偏差的分位数中学习无偏方差。

IQN算法：学习累积折扣奖励的分位数，

同时通过DQN算法：研究累积折扣奖励的均值。

分位数条件矩方法：估计累积折扣奖励的方差，

该方差——挖掘智能体行动选择的一种自然探索奖励，以缓解奖励稀疏问题。值得注意的是，即使估计的分位数因非平稳性而存在偏差，QCM方法估计出的方差仍然是无偏的。（?）

概括和扩展了AlphaGen方法，并可应用于其他非平稳和/或奖励稀疏的环境。

N 只不同股票及其价格和成交量信息

找到一个最优的阿尔法因子池 F（即一组具有协同效应的公式化阿尔法）

构建一个用于预测未来股票收益的线性元阿尔法

公式化阿尔法

序列决策问题逆波兰表示法

RPN ：记录了一个智能体在公式的每个位置选择放置哪个标记时所采取的一系列动作。

这些动作（令牌）主要分为三大类：

操作数 - 提供计算的“原材料”

原始特征：来自历史市场数据的基本元素。
- 例如：Open（开盘价）, High（最高价）, Low（最低价）, Close（收盘价）, Volume（成交量）等。
常数：固定的数值，用于作为运算符的参数。
- 例如：5, 10, -1（如图1中的例子）等。

运算符 - 对“原材料”进行加工的“工具”

一元运算符：对一个操作数进行运算。
- 横截面运算符：在同一时间点，对所有N只股票的某个值进行排序或计算。
  - 例如：Rank（计算横截面排名）, ZScore（计算横截面Z分数）等。
- 时间序列运算符：对单只股票，在其自身的时间序列上进行计算。
  - 例如：Delay（延迟，取前几天的值）, Delta（求差值）等。
二元运算符：对两个操作数进行运算。
- 例如：Add（加 +）, Sub（减 -）, Mul（乘 *）, Div（除 /）等。
高级函数运算符（通常有参数）：结合了时间和横截面维度，功能更复杂。
- 例如：TsRank(数据, 时间窗口d)：计算时间序列d天内的序数排名。如图1所示，它需要两个操作数：一个时间序列数据和一个代表窗口期的常数。

控制令牌 - 定义表达式的开始和结束

BEG：表示表达式的开始。
SEP：表示表达式的结束。当智能体选择此动作时，意味着一个完整的阿尔法公式已经生成。

MDP

以下是MDP核心组件的列表式总结：

状态与动作
- 状态：基于令牌序列的集合 $X$ ，每个状态 $x_{t}$ 对应当前生成的表达式，初始状态为BEG令牌，令牌数≤20（保证可解释性）
- 动作：令牌 $a_{t} \in A$ ，仅 $A$ 的子集对特定 $x_{t}$ 有效（确保令牌序列是合法的阿尔法 RPN）
状态转移核
- 确定性转移：将动作令牌 $a_{t}$ 附加到 $x_{t}$ 末尾生成 $x_{t + 1}$
- 终止条件：若 $a_{t}$ 是SEP令牌，或 $x_{t}$ 达最大长度，回合终止并重置为初始状态 $x_{0}$
奖励
- 未完成令牌序列： $r_{t} = 0$
- 解析出无效阿尔法： $r_{t} = - 1$
- 解析出有效阿尔法：
  1. 新阿尔法加入池，生成扩展池
  2. 拟合线性模型，筛选至多 $P$ 个主成分阿尔法并更新池
  3. 基于更新池生成元阿尔法
  4. 奖励= $更新后元阿尔法IC - 更新前元阿尔法IC$
折扣因子
- 设定 $γ = 1$ （因已限制回合最大长度）
非平稳性
- 根源：阿尔法池更新导致奖励函数变化
- 影响：相似阿尔法后续奖励降低，需大量交互与训练重新学习
奖励稀疏性
- 表现1：仅回合结束（生成新阿尔法）时奖励可能非零，其余为0
- 表现2：市场数据低信噪比，多数阿尔法无意义，奖励常为0
- 影响：智能体训练效率低、不稳定

AlphaQCM 方法

QCM方法学习奖励的无偏方差：分位数

基于 Cornish-Fisher 展开的线性回归

某个动作的分位数 $θ_{k}$ = 动作的平均价值 $Q^{*}$ + 分位数相关系数 $Φ_{k}$ × 矩相关向量 $δ$ + 微小误差 $ω_{k}$ 。

\begin{matrix} (3) & θ_{k} (x, a) = Q^{*} (x, a) + Φ_{k}^{'} δ (x, a) + ω_{k} (x, a), \end{matrix}

其中 $Φ_{k} = (ϕ_{k}, ϕ_{k}^{2} - 1, ϕ_{k}^{3} - 3 ϕ_{k})^{'}$ ，且

δ (x, a) = {(\sqrt{h (x, a)}, \frac{\sqrt{h (x, a)} s (x, a)}{6}, \frac{\sqrt{h (x, a)} [k (x, a) - 3]}{24})}^{'} .

具体来说， $ϕ_{k}$ 是标准高斯分布的 $T_{k}^{*}$ -分位数， $Q^{*} (x, a)$ 、 $h (x, a)$ 、 $s (x, a)$ 和 $k (x, a)$ 分别表示 $Z^{*} (x, a)$ 的均值、方差、偏度和峰度， $ω_{k} (x, a)$ 表示展开误差。

\begin{matrix} (4) & {\hat{θ}}_{k} (x, a) = ζ (x, a) + Q^{*} (x, a) + Φ_{k}^{'} δ (x, a) + ε_{k} (x, a), \end{matrix}

其中 $ζ (x, a)$ 和 $ε_{k} (x, a)$ 分别表示由非平稳性和展开误差引起的确定性偏差和随机残差。

显然，公式(4)可以解释为一个线性回归模型，其中 ${\hat{θ}}_{k} (x, a)$ 和 $Φ_{k}$ 分别作为可观测的响应变量和回归变量，而 $ζ (x, a) + Q^{*} (x, a)$ 、 $δ (x, a)$ 和 $ε_{k} (x, a)$ 则分别对应截距、回归系数和残差。

在手头有 $K$ 个样本 ${({\hat{θ}}_{k} (x, a), Φ_{k})}$ 的情况下，我们可以通过求解上述线性回归模型(4)来获得普通最小二乘估计量 $\hat{h} (x, a), \hat{s} (x, a)$ 和 $\hat{k} (x, a)$ 。在一些温和条件下 $^{4}$ ，这些矩估计量的一致性由以下命题保证：

假设假设 C.1 和 C.2 成立。则当 $K \to \infty$ 时，有 $\hat{h} (x, a) \overset{P}{\to} h (x, a), \hat{s} (x, a) \overset{P}{\to} s (x, a)$ 和 $\hat{k} (x, a) \overset{P}{\to} k (x, a)$ ，其中 $\overset{P}{\to}$ 表示依概率收敛。

尽管 MDP 是非平稳的， $\hat{h} (x, a)$ 仍然是无偏的，而对于传统的基于分位数的方差估计量 $^{5}$ 则无法保证这种无偏性，即使在平稳 MDP 中也是如此（Bellemare et al., 2023）。如 Mavrin 等人 (2019) 所述， $\hat{h} (x, a)$ 同时捕捉了参数不确定性和内在不确定性，这可分别归因于非平稳性和奖励稀疏性。使用 $\hat{h} (x, a)$ 作为探索奖励，我们的智能体倾向于探索最不确定的状态，这些状态也能产生最具信息量的经验，以克服非平稳性和奖励稀疏性带来的挑战。通过在这些信息丰富的经验上进行训练，智能体尽可能减轻了奖励稀疏和非平稳性的负面影响，并有效地从动态环境中学习。

最后，需要注意的是，我们无法使用 QCM 方法估计 $Q^{*} (x, a)$ ，因为估计的截距对应于公式(4)中的 $ζ (x, a) + Q^{*} (x, a)$ ，使得 $ζ (x, a)$ 和 $Q^{*} (x, a)$ 不可识别。因此，我们使用单独的 RL 算法来学习 $Q^{*} (x, a)$ 。在这样一个非平稳 MDP 中，传统的 DRL 算法会产生有偏的 Q 估计，因为它们通过直接对 ${\hat{Z}}_{\hat{θ}, τ} (x, a)$ 取期望来估计 $Q^{*} (x, a)$ 。在非平稳 MDP 中，这种有偏 Q 问题在某种程度上是不可避免的，但使用 QCM 方法可以减轻非平稳性带来的负面影响。根本原因在于，无论是否存在由非平稳性引起的偏差，使用 QCM 方法都能提高训练效率。通过提高训练效率，智能体需要更少的智能体-环境交互和更短的训练时间来重新逼近 $Q^{*} (x, a)$ 。

DRL 主干网络

IQN 算法-学习分位数， DQN 算法-学习 Q 函数。

\hat{Θ} (x_{t}) = F C (ψ (x_{t}) ⊙ ν (τ)) \in R^{| A | \times K},

其中 $\hat{Θ} (x_{t})$ 包含所有 $a \in A$ 和 $k = 1, . . ., K$ 的 ${\hat{θ}}_{k} (x_{t}, a)$ 。有了 $\hat{Θ} (x_{t})$ 后，对于所有 $a \in A$ ，可以通过 QCM 方法计算 $\hat{h} (x_{t}, a)$ 。然后，智能体选择一个探索性动作 $a_{t}$ 以增强训练效率：

\begin{matrix} (5) & a_{t} = \argmax_{a \in A} [\hat{Q} (x_{t}, a) + λ \sqrt{\hat{h} (x_{t}, a)}], \end{matrix}

其中 $\hat{Q} (x, a)$ 由 DQN 算法的 Q 网络计算 $^{6}$ ， $λ$ 是用于控制风险偏好程度的调优参数。可视化说明见图 3。

本文中，Q 网络使用独立的 LSTM 特征提取器和全连接头将 $x_{t}$ 转换为 Q 值：

\hat{Q} (x_{t}) = F C (ψ (x_{t})) \in R^{| A |},

其中 $\hat{Q} (x_{t})$ 包含所有 $a \in A$ 的 $\hat{Q} (x_{t}, a)$ 。

此外，分位数网络使用分位数时序差分误差进行训练（Dabney et al., 2018a），而 Q 网络使用时序差分误差的平方进行训练（Mnih et al., 2015）。为节省篇幅，我们的 AlphaQCM 方法中使用的更多技术细节和超参数在附录 E 中指定，而一些未提及的技术细节与主干网络保持一致。

脚注 $^{4}$ 更多细节参见附录 C。 $^{5}$ 传统的基于分位数的方差估计量定义见附录 D。 $^{6}$ （注：原文此处标注为“algorithm”，未额外脚注）

核心挑战	原方法 (AlphaGen) 的问题	AlphaQCM 的解决方案	解决之道核心思想
1. 奖励稀疏性	只依赖稀疏的外在奖励：智能体只有生成一个完整阿尔法后，才能获得一个可能非零的奖励（大部分时间为0）。这导致探索动力不足，容易陷入局部最优，在广阔的搜索空间中效率低下。	引入“内在探索奖励”：利用分布强化学习得到的回报方差，作为一个额外的探索信号。	“好奇心驱动探索”：不仅为“找到金子”（高回报）而学习，也为“探索未知区域”（高不确定性）而学习。即使一个动作的平均回报（Q值）不高，但只要其结果不确定性大（方差高），就值得尝试，从而主动地在稀疏奖励环境中寻找有价值的信号。
2. 非平稳性	忽视环境变化：其学习模型（如Q函数）基于历史经验，当阿尔法池更新导致奖励函数改变后，这些经验会过时，但模型无法快速感知和适应这种变化，导致学习不稳定、效率下降。	使用无偏方差作为环境变化的“传感器”：通过QCM方法，从可能带有偏差的分位数中计算出无偏的方差估计。这个无偏方差能可靠地指示环境何时发生了变化。	“拥有一个可靠的指南针”：当环境规则改变时，许多状态-动作对的回报分布会变得不稳定（方差骤增）。AlphaQCM能通过其无偏方差的剧增，敏锐地探测到这种变化，并立即引导智能体加强对变化区域的探索，从而快速重新学习新的规则，适应非平稳的环境。

实验

https://github.com/ZhuZhouFan/AlphaQCM

三个真实市场数据集以评估其实证性能，同时与基线方法（如AlphaGen方法和基于GP的方法）进行比较

信息系数值

消融研究

中国 A 股市场数据集上进行，以捕捉未来 20 天的股票收益

评估所考虑金融系统的复杂性对性能的影响

三个不同的股票池：(1) 最大的 300 只股票（沪深 300），(2) 最大的 500 只股票（中证 500），以及 (3) 在上海和深圳证券交易所上市的所有股票（全市场）

数据集中涉及的股票越多，发现协同公式化阿尔法因子的挑战就越大，因为系统变得更加复杂和混沌

每个数据集按时间顺序被划分为训练集（2010/01/01 至 2019/12/31）、验证集（2020/01/01 至 2020/12/31）和测试集（2021/01/01 至 2022/12/31）

四类基线方法进行比较：
(1) Alpha101（人工设计的公式化阿尔法）：将阿尔法池固定为 Kakushadze (2016) 提供的公式化阿尔法，并拟合一个线性模型以形成元阿尔法。
(2) MLP, XGBoost, LightGBM（基于机器学习的非公式化阿尔法）：使用 MLP 模型、XGBoost 模型或 LightGBM 模型来形成元阿尔法。
(3) GP w/o filter, GP w/ filter（基于遗传编程的公式化阿尔法）：使用 GP 方法生成表达式，并应用表现最优的前 P 个阿尔法（不带或带互信息系数过滤器）来形成元阿尔法。
(4) PPO w/ filter, AlphaGen（基于强化学习的公式化阿尔法）：使用带有互信息系数过滤器的 PPO 算法或 AlphaGen 方法来寻找最优阿尔法池，然后形成线性元阿尔法。

评分维度	核心指标 / 规则	目的
核心性能	测试集 IC 均值（越高越好）	衡量阿尔法的预测能力
结果可靠性	IC 标准差（越小越好）	衡量方法的稳定性
泛化能力	跨股票池 IC 一致性（越稳定越好）	衡量方法在复杂市场中的适应性
实用价值	可解释性（公式化 > 非公式化）	确保方法能应用于实际金融场景
对比公平性	验证集统一调优超参数	保证不同方法的对比公平

关键：从可能存在偏差的分位数中推导出方差的无偏估计

IQN算法作为主干网络来获取分位数，同时使用DQN算法来近似Q函数

结果

在习得的Q函数与方差引导下，AlphaQCM能够有效克服非平稳性与奖励稀疏性，以更高效率在广阔的公式化阿尔法搜索空间中进行探索

现象

优于现有竞争模型，尤其是在处理包含大量股票的大规模数据集时表现尤为突出。

机制机理

项目	内容
论文标题	AlphaQCM: Alpha Discovery in Finance with Distributional Reinforcement Learning
研究背景	量化因子（alpha）可解释性强但难自动搜索； GP 方法搜索空间指数爆炸； RL 搜索方法 AlphaGen 存在非平稳性与奖励稀疏问题。
核心贡献	① 首次使用分布式 RL + QCM 解决非平稳/稀疏奖励 MDP； ② 设计无偏方差作为探索奖励； ③ 构建 alpha 池动态更新机制； ④ 提高大规模股票集（全市场）上的因子发现能力。
数据与特征	中国 A 股三种股票池（CSI 300、CSI 500、全市场），历史 OHLCV，构造成 tokens（RPN 逆波兰表达式）组成因子。
方法技术路线	- 将因子表达式 token 序列建模为状态； - 动作是选择下一个 token； - 奖励是 alpha 池加入新因子后 meta-alpha 的 IC 改进； - IQN 估计分位数 → QCM 估方差 → 用方差奖励促进探索； - DQN 估计 Q 值。
实验结果	在三个股票池中取得最高 IC，显著优于 AlphaGen、GP、MLP/XGBoost 等。尤其在大规模股票池中优势更明显。
关键启示	非平稳/稀疏奖励是金融强化学习中的核心瓶颈；使用“方差作为探索信号”能有效提升效率； DRL 能进行因子挖掘并保持可解释性。
局限性	Q 值仍可能偏置；训练成本高；依然存在表达式可解释性受限、依靠复杂 token 结构。
未来方向	可加入 LLM 进行 token 生成；加入因果图模型提升可解释性；更丰富的 alpha 运算子空间。